I.
The Prisoner's Dilemma is something that you've almost certainly already read about if you have the slightest interest in psychology or economics. When I looked at the half formed idea for a post I had in my 'Blog Posts' Trello bucket[1] I almost scrapped it for that reason.
However! I intend to explore the Prisoner's Dilemma in a little more depth than most students would if forced to in class, and everyone lives in their own little bubble - something obvious to you is news to me, or vice versa, on a daily basis.
 ]
]
Saying 'what kind of an idiot doesn't know about the Yellowstone supervolcano' is so much more boring than telling someone about the Yellowstone supervolcano for the first time.
Source: https://xkcd.com/1053/
II.
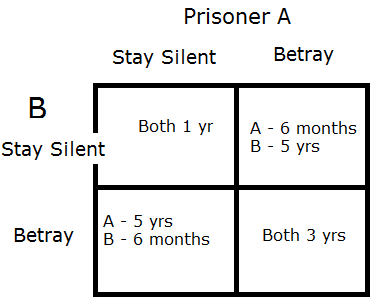
The Prisoner's Dilemma is the following situation. Two people have been taken in for questioning over a crime. They can choose to say nothing, or to betray their partner in exchange for a shorter sentence. If both partners betray each other, they each get a sentence of 3 years in gaol. If one partner betrays the other, he gets a reduced six month sentence and his partner gets the maximum sentence of 5 years. If neither betrays the other, they both serve a sentence of 1 year. This is illustrated in the below graph:

The dilemma is, as a prisoner, should you choose to defect, or to cooperate? What is the optimal strategy?
From a purely selfish perspective, the incentive is to defect. No matter what the partner does, defecting is the best choice. If they choose to cooperate, you can get a shorter sentence by defecting. Similarly if they defect, your incentive is to defect because it will shorten your sentence[2].
This feels somehow wrong, because your supposed optimal payoff, if both players take the same approach, results in a worse payoff than two other payouts that are possible. But in the simplest version of the game, mathematically you should defect, and that means a suboptimal payout when both players use the same strategy. This does play out often in real life.
Examples:
- Predatory violence - When harming someone to take some gain from them, a predator is also running the risk that they will fight back and both will lose more than they gain.
- Theft - When it is a one off situation, immoral acts like theft make a certain logical sense - if you know you'll never see the person again then why not defect? The legal system exists to incentivize against this but there's still the issue of getting caught.
- Women wearing makeup is a Prisoner's Dilemma that has settled into a defect/defect equilibrium. If all women agreed to not wear makeup, then they'd all collectively save half an hour a day of time. However there is a huge incentive for any individual woman to 'defect' and wear makeup to gain an attractiveness advantage over those without it, hence forcing everyone to 'defect'.
- Military Spending - If everyone agreed not to have a military, we could all reap the gains from using our military expenditure elsewhere. However we can't trust all other nations to do so and it's too easy to defect, so yet again we end up in the defect/defect equilibrium.
So we get stuck in this undesirable situation that is somehow still perfectly logical. That is unless you throw the rulebook out the window like this guy:
What he was doing in the video, by the way, was to change the calculus of the game for his opponent. In the initial version of the game the payoff is Split = maybe half maybe nothing, Steal = maybe all maybe nothing. If his opponent took him at his word then it becomes Split = half, Steal = nothing, making Split the only correct choice.
So, in the basic game, we have two equilibria:
- The first is the defect/defect approach.
- The second is the cooperate/cooperate approach, which unfortunately doesn't often happen because in a game where you have reason to believe your opponent will cooperate, the logical move is to defect.
This leaves us with a bit of a paradox - the simple game always results in defection, yet in real life that isn't what happens - there are some situations like the ones above but by and large people manage to get along. What is the model missing?
III.
There is an extension on the Prisoner's Dilemma called the Iterated Prisoner's Dilemma. It's called 'iterated' because you play over many iterations, either a set number known by both players, a random number of turns, or an infinite number of turns[3]. So instead of playing a one-off dilemma, it happens repeatedly.
A model for this might be the 'grocer and supplier' model. In this model the grocer wants his supplier to deliver quality goods. If he gets quality goods, he makes some profit, the supplier makes some profit, they go away away happy. The supplier however can defect by supplying cheap goods to the grocer, pocketing the difference in change. The grocer can similarly defect by reporting the goods as a return, costing the supplier money.
This represents an Iterated Prisoner's Dilemma because although the numbers in the above grid are still the same as before, it is being played by the two participants repeatedly. There is a history and any defection can be remembered and punished by the other participant. Because of this, you can no longer defect and get away with it, your partner will have lost trust from your initial defection. This results in an incentive not to defect, but to instead cooperate in exchange for your partner cooperating on future turns.[4]
Real world examples:
- Any mutual partnership similar to the one described above - where cooperation gets you both some gains, and either of you can defect on the other for a larger, one-time payoff - resembles an Iterated Prisoner's Dilemma. This is very common between businesses.
- Diplomacy between countries also follows this model. While military spending is in a negative equilibrium, actual relationships between countries have been by and large peaceful since the end of world war 2, largely because of the huge costs of being defected on and the possibility of retaliation to anyone who defects.
So that's the basic setup of the Prisoner's Dilemma and it's analogue to real life. It turns out there is plenty more to say[5] about it and more to the history of the game which I'll cover in the next post.
I have a list of Trello cards just for blog posts. They usually start as just a title or half formed idea like 'Prisoner's dilemma - history, extensions, analogues.' Over time I'll add notes, tweaks, and comments, and reorder sections as the idea comes back up, until it eventually gets turned into a blog post - or if it's a really shitty idea - deleted. ↩︎
Even in a version where the sentence is 5 years either way if you get defected on, you can argue that defecting is the optimal choice as it doesn't lessen your sentence and does put your opponent in a worse position. ↩︎
In the purely theoretical sense; you cant actually program this in a computer. ↩︎
There are still some slight differences if the horizon is known or unknown. If you know there will be 10 turns, there is no reason not to defect on the tenth. And if you know your opponent knows this, you should defect on the ninth... etc etc. Whereas with an unknown horizon your best bet is to assume it is infinite. ↩︎
WE CAN GO DEEPER ↩︎